해당 글은 ISLR 2nd Edition 영문판을 학습하고 번역한 글 입니다. 따라서, 일부 오역이 있을수도 있습니다.
2.1 What is Statistical Learning?
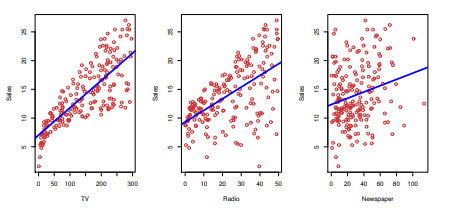
- 그림은 통계 학습을 설명하기 위해 광고 단가 대비 매출을 나타낸다.
- 또한, 매출을 예측하기 위해 선형 회귀를 통해 각각의 그래프를 fit을 진행한다.
- 각각의 그래프의 파랑 추세선을 보았을 때 TV가 가장 좋은 효율을 보여준다.
- 출력 변수를 , 입력 변수를 X로 가정하였을 때 X는 광고 단가, Y는 매출이다.
일반적인 식으로 표현 하자면 아래와 같이 표현된다.
$$Y = f(x)+ϵ$$
- 식에서 $f$는 X와 Y의 관계를 규정 짓는 함수이며, $ϵ$는 x와는 관계 없는 추가적인 noise이며, 평균은 0이다.
- 본질적으로 통계적 학습은 $f$를 추정하기 위한 일련의 접근 방식을 의미한다.
2.1.1 why estimate f?
- $f$를 추정하는 이유는 예측과 추론 두 가지로 구성된다.
Prediction
- 많은 상황에서 X는 알지만 Y는 알기 힘들다.
- 따라서 Y값을 얻기 위해 오차 항의 평균이 0인 점을 이용하여 예측이 가능하다.
- 입력 변수들을 사용하여 출력 변수 값을 예측하기를 원하는 경우 사용
$$\hat{Y} =\hat{f},$$ - 식에서 $\hat{f}$는 $f$에 대한 추정치를 나타내고 $\hat{Y}$는 $Y$에 대한 결과 예측을 나타낸다.
- 값을 예측하는 경우 일반적으로 $\hat{f}$의 Black Box 로 생각한다. 예측의 정확성만 좋다면 내부의 형식은 상관이 없다.
$$ E(Y-\hat{Y})^2 \;= E[f(x)+ϵ-\hat{f}(x)]^2\ =\overbrace{[f(x)-\hat{f}(x)]^2}^{\rm Reducible}+\overbrace{Var(ϵ)}^{\rm Irreducible}$$
- 식에서 $[ f(x) -\hat{f}(x)]^2$ 는 축소 가능한 오차(reducible error), $Var(ε)$는 축소 불가능한 오차(irreducible error)이다.
- 적절한 통계기법을 사용해서 f를 추정함으로써 f̂의 정확성은 개선이 가능하지만, ε에 의해 유입된 오차를 줄일 수는 없다.
- 축소 불가능한 오차는 Y에 대한 예측 정확도의 상한선이며, 이 경계는 실제로 거의 항상 알려있지 않다.
- 책의 초점은 축소 가능한 오차를 최소로 하며 $f$를 추정하는 기법에 대해 다룬다.
Inference
- 어떤 과정으로 이런 일이 일어나는지 내부 논리/구조를 파악도 필요하다. 이때, 모델을 추론하기 위해 $f$를 추정 한다.
- 입력 변수와 설명 변수 사이의 인과관계를 파악하고자 하는 경우 사용
- 응답과 관련된 예측 변수는 무엇인가?
- 사용 가능한 입력 변수(X)의 작은 부분만이 실질적으로 출력 변수(Y) 와 관련된 경우가 많다.
- 반응과 각 예측 변수 사이의 관계는 무엇인가?
- 일부 입력 변수(X)는 값이 클수록 출력 변수(Y) 값이 더 크다는 점에서 Y와 양의 관계를 가질 수 있습니다. 다른 예측 변수는 반대 관계를 가질 수 있습니다.
- $f$의 복잡성에 따라 응답과 주어진 입력 변수 간의 관계는 다른 입력 변수의 값에 따라 달라질 수도 있습니다.
- Y와 각 예측 변수 간의 관계를 선형 방정식을 사용하여 적절하게 요약할 수 있나? 아니면 관계가 더 복잡한가?
- 일반적으로 $f$를 추정하는 대부분의 방법은 선형 형식를 사용했다.
- 종종 실제 관계는 더 복잡하다. 따라서, 이 경우 선형 모델은 입력 변수와 출력 변수 간의 관계를 정확하게 표현하지 못할 수 있다.
- 궁극적인 목표가 예측인지, 추론인지, 아니면 이 둘의 조합 인지에 따라 $f$를 추정하는 방법이 다를 수 있다.
2.1.2 How do we estimate f?
- 책을 통해 다양한 선형/비선형 모델을 보겠지만 몇가지 공통점이 있다.
- n개의 데이터가 주어진다면 이를 학습 데이터라고 부른다.
- 목적은 통계 학습을 학습 데이터에 잘 적용해서 함수$\hat{f}$를 찾는 것이다.
- 잘 찾아졌다면 추가적인 데이터 입력에도 대략적으로 라도 $Y=\hat{f}(X)$가 성립가능하다.
모수적 방법 (Parametric Methods)
- 함수의 형태를 특정 모양으로 모양에 대해 가정한다.
$$ f(X)=β_0+β_1X_1+β_2X_2+...+β_pX_p $$
- 위와 같은 식이라고 가정한다면, 이는 선형 모델이라고 부를 수 있다.
- 모델을 선택한 후, 훈련 데이터를 통해 모형을 fit하거나 훈련시키고 파라미터 집합을 추정한다.
$$ Y \approx β_0+β_1X_1+β_2X_2+...+β_pX_p $$
- 위와 같은 모델의 매개변수 값을 찾고자 하는 방법이다.
- 장점
- $f$를 추정하는 문제를 단순화하며, 임의의 함수$f$를 적합 시키는 것보다 파라미터를 추정하는 것이 일반적으로 쉽다.
- 단점
- 선택한 모델이 알려지지 않은 $f$의 실제 형태와 보통은 맞지 않다.
- 복잡한(유연한) 모델을 선택하면 데이터에 대한 과적합이 뒤따른다.
비모수적 방법 (Non-parametric Methods)
$f$ 함수 형태에 대해 명시적인 가정을 하지 않고 $f$를 추정하는 방법
- 장점: 추정한 $f$가 실제 $f$와 많이 달라질 위험을 방지
- 단점: 아주 많은 수의 관측치가 필요
2.1.3 The Trade-Off Between Prediction Accuracy and Model Interpret ability
- 일반적으로 통계 학습 모델의 복잡도와 해석 가능성은 trade-off 관계에 있다.
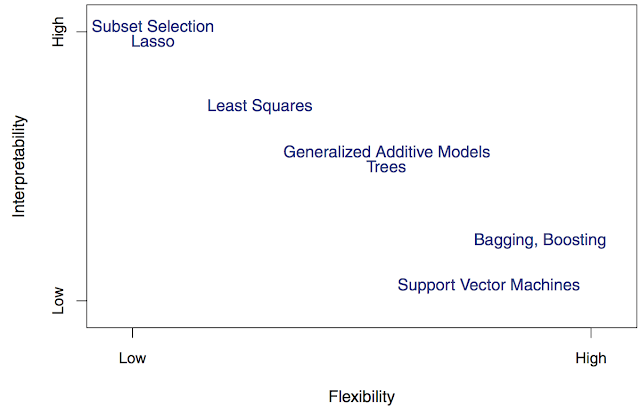
- 그림에서 X축은 모델의 복잡도, Y축은 해석 가능성을 나타낸다.
- 이때 복잡한 모델이 성능은 잘 나올 수 있지만, 추론을 하기가 어려워서, 모델이 어떻게 예측을 잘하였는지 해석하기가 어렵다.
- 추론에 중점을 두는 경우
- 제한적인 모델이 훨씬 해석하기 쉬우므로 덜 복잡한 방법을 사용하는 것이 좋은 선택일 수 있다.
- 예측에 중점을 두는 경우
- 복잡한 모델이 더 적합할 수 있다.
- 추론에 중점을 두는 경우
- 하지만 무조건 모델의 복잡도가 높다고 해서 좋은것은 아닌다. 이는 과적합의 문제가 뒤따른다.
2.1.4 Supervised vs Unsupervised Learning
통계 학습은 출력 변수의 존재 유무에 따라 지도 학습 / 비지도 학습으로 나뉜다.
지도학습 (Supervised)
- 지도 학습은 말 그대로 정답이 있는 데이터를 활용해 데이터를 학습 시키는 것입니다. 입력 값(X data)이 주어지면 입력 값에 대한 Label을 주어 학습 시킨다.
- 대표적으로 분류, 회귀 문제가 있습니다.
비지도학습 (Unsupervised)
- 지도 학습과는 달리 정답 라벨이 없는 데이터를 비슷한 특징끼리 군집화 하여 새로운 데이터에 대한 결과를 예측하는 방법을 비지도 학습 이라고 한다.
- 라벨링 되어있지 않은 데이터로부터 패턴이나 형태를 찾아야 하기 때문에 상대적으로 어려운 경향이 있다.
- 비지도 학습의 대표적인 종류는 클러스터링(Clustering)이 있습니다.
2.1.5 Regression vs Classification Problems
- 입력 및 출력 변수는 수치형 or 범주형 값으로 나눌 수 있다.
- 수치형 값은 사람의 나이나 키, 온도, 가격처럼 연속적인 값을 의미합니다.
- 범주형 값은 제품의 브랜드 (A, B, C), 어떤 병에 걸려있는지 아닌지 (True, False) 등의 특징은 숫자로 표현되지 않는 qualitative 값입니다.
- 회귀 (Regression)
- 출력 변수가 수치형 변수일 때 사용하는 통계 학습 방법
분류 (Classification )
- 출력 변수가 범주형 변수일 때 사용하는 통계 학습 방법
- 하지만 데이터의 도메인이나 Task가 무엇이냐에 따라 분류 문제도 회귀 모델을 써서 풀 수 있고, 반대도 가능하다.
2.2 Assessing Model Accuracy
- 통계 학습은 많은 접근 방법 들이 존재한다. 하지만 특정 방법의 모델이 가장 좋다고는 할 수 없다.
- 특정 데이터 세트에 대해 A라는 방법이 잘 동작 수 있을지언정, 유사한 다른 데이터에서는 B라는 방법이 더 잘 동작할 수 있다.
- 따라서 주어진 데이터 집합에 대해 어떤 방법이 최상의 결과를 생성하는지 결정하는 것이 중요한 작업이다.
- 본 장에서는 특정 데이터 세트에 대한 통계적 학습 방법을 선택할 때 가장 중요한 요점에 대해 설명한다.
2.2.1 Measuring the Quality of Fit
- 데이터 세트에 대한 통계적 학습 방법의 성능을 평가하려면 예측이 실제로 관찰된 데이터와 얼마나 잘 일치하는지 측정할 방법이 필요하다.
- 즉, 주어진 정답 값에 대한 예측된 값이 얼마나 유사 한지를 수치화 해야 한다.
- 회귀에서 가장 일반적으로 사용되는 성능 지표는 평균 제곱 오차(MSE)이다.
$$ MSE = {1\over n} \sum_{i=1}^{n} (y_i − \hat{f}(x_i))^2, $$
- 식에서 $\hat{f}(x_i)$는 $\hat{f}$가 i번째 관측 값에 대한 예측이다.
- MSE는 예측된 값이 실제 값에 매우 가깝다면 작을 것이고 일부 관측치에 대해 예측된 반응과 실제 반응이 크게 다를 경우 클 수 있다.
- 일반적으로 모델이 복잡성이 높을 수록 Train MSE는 낮아 집니다. 하지만 이는 훈련 데이터 국한되어 적합하다.
- 그러나 실 세계에서는 Train 데이터에 국한되지 않고 새로 유입되는 데이터 즉, Test데이터의 MSE가 더 중요하다.
- 그렇다면 데이터 세트에 적합한 통계 모델을 찾기 위해서는 Tset MSE의 성능을 보고 모델을 정할수 있다. 하지만 Test 데이터가 없다면 Train과 Test 데이터는 밀접한 관련이 있기 때문에 Train MSE를 고려하면 되지 않나라고 할 수 있다.
- 하지만 이는 근본적인 문제가 있는데 이는 많은 통계적 방법이 훈련 세트 MSE를 최소화하기 위해 coefficients를 추정한다는 것이다.
- 이러한 방법의 경우 Train MSE는 매우 작을 수 있지만 Test MSE는 큰 경우가 많다.
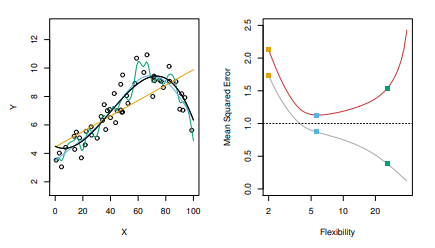

- 위의 그림은 모델의 복잡성과 MSE 관계를 보여준다.
- 왼쪽 그림의 주황색선 과 같은 경우는 모델의 복잡성이 가장 떨어지는 모델이다. 또한, 녹색과 같은 경우는 가장 복잡한 모델을 나타낸다.
- 이때, MSE의 결과를 보자면 Train MSE와 같은 경우는 모델의 복잡성이 가장 높은 녹색이 가장 좋은 모습을 보인다. 하지만 Test MSE와 극명한 차이를 보여준다.
- 여기서 주황색과 녹색의 중간정도의 복잡성을 보여주는 파란색과 같은 경우는 Train MSE는 녹색과 비교했을 때 다소 높지만 Test MSE는 수평 점선에 가장 근접한 MSE의 성능을 나타낸다.
- 즉, 모델이 복잡성이 높다고 Test의 성능은 좋지 않으며 과적합의 요인이 될 수 있다.

- 위의 그림은 비선형적인 예를 보여주는데 훈련 및 테스트 MSE 곡선은 여전히 동일한 일반 패턴을 나타내지만 이제 테스트 MSE가 천천히 증가하기 시작하기 전에 두 곡선 모두에서 급격한 감소가 있다.
- 실제 $f$가 선형적이라면, 덜 복잡한 모델의 Test MSE가 복잡한 모델보다 나을 것이다.
- 실제 $f$가 비선형적이라면, 복잡한 모델의 Test MSE가 더 나을 것이다.
- Test MSE가 최소가 되는 모델에 대응하는 복잡성 수준은 데이터에 따라 상당히 다르다.
- Test MSE를 최소로 하기 위해 교차검증(cross-validation)을 사용할 수 있다.
2.2.2 The Bias-Variance Trade-Off
- Test MSE 곡선이 U모양인 이유는, 분산과 편향 두 가지 상충되는 성질 때문이다.
$$ E(y_0-\hat{f}(x_0))^2 = Var(\hat{f}(x_0))+[Bias(\hat{f}(x_0))]^2+Var(ϵ)\qquad [2.7] $$
$$ Expected\; Test \; MSE = Variance+ Bias^2 + Error\; Term $$
- 위의 식에서 $Var(ϵ)$(irreducible error)는 낮출 수 있는 방안이 없다.
- 따라서, Test MSE의 기댓값을 최소화 하는 것을 목표로 낮은 분산과 낮은 편향을 같이 가져 갈수 있는 통계 학습 방법을 선정해야 한다.
- 이때 , 분산과 편향은 다음과 같다.

- 편향(Bias)
- 복잡한 실 세계 문제를 훨씬 단순한 모델로 근사시킴으로 인해 발생되는 오차
- 비선형적인 형태를 띄는 데이터를 선형 모델로 근사하더라도 아무리 많은 데이터가 존재해도 정확한 추정치를 생성하는 것은 어렵다.
- 일반적으로 복잡성이 높을 수록 편향이 적다.
- 분산(Variance)
- 데이터 셋의 변동에 따른 (즉, 데이터가 바뀜에 따라) $\hat{f}$의 변화의 정도
- 일반적으로 복잡성이 높을수록 분산도 높다. 이는 훈련하는 데이터 셋에 과도하게 적합하려 하므로, 다른 데이터셋 을 훈련시킬 경우 $\hat{f}$이 많이 변동될 수 있다. (데이터 포인트 중 어느 하나를 변화시키면 추정치 $\hat{f}$이 크게 변할 수 있음을 의미)
- 분산과 편향의 상대적인 변화율은 Test MSE가 증가하는지 감소하는지를 결정한다.
- 그림 2.9–2.11의 오른쪽 패널에서 테스트 MSE가 감소한 후 테스트 MSE가 증가하는 패턴이다.
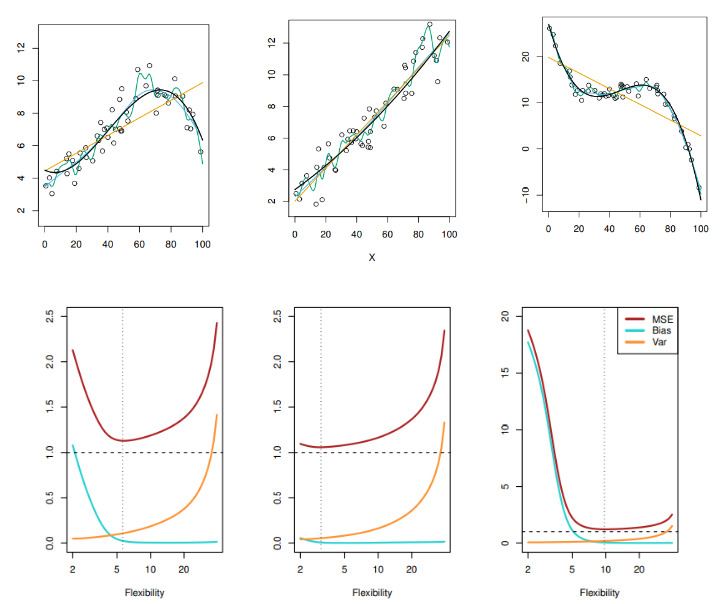

- 통계 방법의 유연성을 증가시킴에 따라 편향이 분산보다 빠르게 감소한다.
- 하지만 어떤 지점에서 유연성 증가는 편향에 크게 영향이 없지만 분산은 크게 증가시키기 시작한다.
- 실제 f가 선형에 가까울수록 모델이 유연해짐에 따라 분산의 증가폭이 커지므로 덜 유연한 모델을 선택하는 것이 좋다.
- 실제 f가 비선형적 일수록 모델이 유연해짐에 따라 편향의 감소폭이 커지므로 유연한 모델을 선택하는 것이 좋다.
2.2.3 The Classification Setting
- 분류의 평가 방법으로 일반적으로 사용되는 Error rate를 계산한다.
$$ {1\over n}∑_{i=1}^n=I(y_i≠\hat{y}_i) $$
- 위의 식에서 $\hat{y}_i$ 는 i번째 입력 데이터을 통한 모델의 예측값을 나타낸다. 또한 $I()$는 Indicator 함수(지시 함수, 표시 함수)라고 부르며, $I(true)=1,I(false)=0$으로 정의된다.
- 따라서 Error rate는 전체 예측 중 잘못 예측(분류)한 비율을 나타낸다.
베이즈 분류기(Bayes Classifier)
- 베이즈 분류기는 아래의 식을 (Bayes rule) 최대화하는 클래스 $j$를 고르는 방법이다.
$$ Pr(Y = j|X = x_0) $$
- 예를 들어 관측된 설명변수 벡터 $x_0$가 주어진 경우, Y=j 인 조건부 확률
- 조건부 확률이란 ?
- 이미 사건이 발생한 조건에서 다른 사건이 발생할 확률
- 베이즈 오차율: $1 - E(maxPr(Y = j | X)),$ 오차율의 평균값
K-최근접 이웃(KNN)
- KNN은 학습 데이터의 X를 통해 테스트 데이터가 입력되었을 때 K의 갯수에 따른 주변 데이터의 클래스를 확인하고 다수결을 통해 예측값을 정하는 직관적인 방법이다.
- K의 선택은 KNN 분류기에 영향을 미친다.
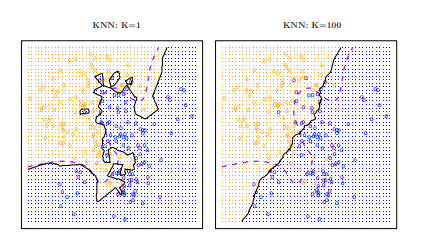
- K = 1일 때 결정경계는 지나치게 유연하고 베이즈 결정 경계와 맞지 않는 데이터 패턴들을 발견한다. (편향은 낮지만 분산은 높음)
- K = 100일 때 결정경계가 덜 유연해지고 점점 선형에 가까워 진다. (분산은 낮지만 편향은 높음)
- 아래의 그림을 확인해보면 K 의 갯수 선택도 모델의 성능에 영향을 미친다 . 각각의 MSE 결과를 보면서 적당한 K의 수를 정한다.

- 회귀와 분류에서 올바른 수준의 모델 유연성을 선택하는 것은 통계 학습방법 성공에 아주 중요하다.
Inference
- 어떤 과정으로 이런 일이 일어나는지 내부 논리/구조를 파악도 필요하다. 이때, 모델을 추론하기 위해 $f$를 추정 한다.
- 입력 변수와 설명 변수 사이의 인과관계를 파악하고자 하는 경우 사용
- 응답과 관련된 예측 변수는 무엇인가?
- 사용 가능한 입력 변수(X)의 작은 부분만이 실질적으로 출력 변수(Y) 와 관련된 경우가 많다.
- 반응과 각 예측 변수 사이의 관계는 무엇인가?
- 일부 입력 변수(X)는 값이 클수록 출력 변수(Y) 값이 더 크다는 점에서 Y와 양의 관계를 가질 수 있습니다. 다른 예측 변수는 반대 관계를 가질 수 있습니다.
- $f$의 복잡성에 따라 응답과 주어진 입력 변수 간의 관계는 다른 입력 변수의 값에 따라 달라질 수도 있습니다.
- Y와 각 예측 변수 간의 관계를 선형 방정식을 사용하여 적절하게 요약할 수 있나? 아니면 관계가 더 복잡한가?
- 일반적으로 $f$를 추정하는 대부분의 방법은 선형 형식를 사용했다.
- 종종 실제 관계는 더 복잡하다. 따라서, 이 경우 선형 모델은 입력 변수와 출력 변수 간의 관계를 정확하게 표현하지 못할 수 있다.
- 궁극적인 목표가 예측인지, 추론인지, 아니면 이 둘의 조합 인지에 따라 $f$를 추정하는 방법이 다를 수 있다.
'Statistics > ISLR 2nd Edition' 카테고리의 다른 글
| ISLR 2nd Edition - 5장 (0) | 2021.11.01 |
|---|---|
| ISLR 2nd Edition - 4장 (0) | 2021.11.01 |
| ISLR 2nd Edition - 3장 (0) | 2021.11.01 |
